Discrete Distribution / Distribusi diskrit adalah distribusi probabilitas yang menggambarkan kemunculan hasil-hasil yang terpisah (dapat dihitung secara individual), seperti 1, 2, 3, ya, tidak, benar, atau salah. Distribusi binomial, misalnya, adalah Discrete Distribution yang mengevaluasi probabilitas hasil “ya” atau “tidak” yang terjadi pada sejumlah percobaan tertentu, dengan mempertimbangkan probabilitas kejadian dalam setiap percobaan—seperti pelemparan koin seratus kali dan hasilnya adalah “kepala”.
Distribusi statistik dapat bersifat diskrit atau kontinu. Distribusi kontinu dibangun dari hasil yang berada pada suatu kontinum, seperti semua bilangan yang lebih besar dari 0 (termasuk bilangan yang desimalnya berlanjut tanpa batas, misalnya pi = 3,14159265…). Secara keseluruhan, konsep Discrete Probability Distribution dan kontinu serta variabel acak yang dijelaskannya merupakan landasan teori probabilitas dan analisis statistik.
Memahami Discrete Distribution
Distribusi adalah konsep statistik yang digunakan dalam penelitian data. Mereka yang ingin mengidentifikasi hasil dan probabilitas suatu studi tertentu akan memetakan titik data terukur dari kumpulan data, sehingga menghasilkan diagram distribusi probabilitas. Banyak bentuk diagram distribusi probabilitas yang dihasilkan dari studi distribusi, seperti distribusi normal (“kurva lonceng”).
Para ahli statistik dapat mengidentifikasi perkembangan distribusi diskret atau kontinu berdasarkan sifat hasil yang akan diukur. Berbeda dengan distribusi normal, yang bersifat kontinu dan memperhitungkan setiap kemungkinan hasil sepanjang garis bilangan, Discrete Distribution dibangun dari data yang hanya dapat mengikuti serangkaian hasil yang terbatas atau diskrit.
Discrete Distribution mewakili data dengan jumlah hasil yang dapat dihitung, yang berarti bahwa hasil potensial dapat dimasukkan ke dalam daftar dan kemudian dibuat grafiknya. Daftarnya mungkin terbatas atau tidak terbatas. Misalnya, ketika menentukan distribusi probabilitas sebuah dadu dengan enam sisi bernomor, daftarnya adalah 1, 2, 3, 4, 5, 6. Jika Anda melempar dua dadu, peluang untuk melempar dua angka enam (12) atau dua satu (dua) jumlahnya jauh lebih sedikit dibandingkan kombinasi lainnya; pada grafik, Anda akan melihat probabilitas keduanya diwakili oleh batang terkecil pada grafik.
jenis Discrete Probability Distribution
Discrete Probability Distribution yang paling umum meliputi binomial, Bernoulli, multinomial, dan Poisson.
Binomium
Distribusi probabilitas binomial adalah distribusi yang hanya mempunyai probabilitas dua hasil. Dalam distribusi ini, data dikumpulkan dalam salah satu dari dua bentuk setelah percobaan berulang dan diklasifikasikan menjadi berhasil atau gagal. Umumnya memiliki himpunan terbatas yang hanya berisi dua kemungkinan hasil, seperti nol atau satu. Misalnya, melempar koin akan memberi Anda daftar {Heads, Tails}.
Distribusi binomial digunakan dalam model penetapan harga opsi yang mengandalkan pohon binomial. Dalam model pohon binomial, aset dasar hanya dapat bernilai tepat satu dari dua kemungkinan nilai—dengan model tersebut, hanya ada dua kemungkinan hasil pada setiap iterasi—pergerakan ke atas atau ke bawah dengan nilai yang ditentukan.
Bernoulli
Distribusi Bernoulli mirip dengan distribusi binomial karena terdapat dua kemungkinan hasil. Satu percobaan dilakukan, sehingga hasil dalam distribusi Bernoulli diberi label nol atau satu. Angka satu menunjukkan keberhasilan, dan angka nol berarti kegagalan—satu percobaan disebut percobaan Bernoulli.
Jadi, jika Anda menggunakan satu kelereng hijau (untuk keberhasilan) dan satu kelereng merah (untuk kegagalan) dalam mangkuk tertutup dan memilih tanpa melihat, Anda akan mencatat setiap hasil sebagai nol atau satu, bukan keberhasilan atau kegagalan untuk sampel Anda. Distribusi Bernoulli digunakan untuk melihat kemungkinan suatu investasi akan berhasil atau gagal.
Multinomial
Distribusi multinomial terjadi ketika terdapat kemungkinan lebih dari dua hasil dengan jumlah yang banyak. Misalnya, Anda memiliki mangkuk tertutup dengan satu kelereng hijau, satu merah, dan satu kelereng kuning. Untuk pengujian Anda, catat berapa kali Anda memilih secara acak masing-masing kelereng untuk sampel Anda.
Distribusi Poisson
Distribusi Poisson menyatakan peluang terjadinya sejumlah kejadian dalam jangka waktu tertentu.
Distribusi Poisson adalah Discrete Distribution yang menghitung frekuensi kemunculan sebagai bilangan bulat, yang daftarnya {0, 1, 2, …} tidak terbatas. Misalnya, Anda memiliki mangkuk tertutup dengan satu kelereng merah dan satu kelereng hijau, dan periode yang Anda pilih adalah dua menit. Tes Anda adalah mencatat apakah Anda memilih kelereng hijau atau merah, dengan warna hijau menunjukkan keberhasilan. Setelah setiap pengujian, masukkan kembali kelereng ke dalam mangkuk dan catat hasilnya. Dalam model ini, distribusi akan memplot hasil selama periode waktu tertentu, yang menunjukkan seberapa sering warna hijau dipilih. Distribusi Poisson biasanya digunakan untuk memodelkan data keuangan yang penghitungannya kecil dan sering kali nol. Misalnya, ini dapat digunakan untuk memodelkan jumlah perdagangan yang biasanya dilakukan investor pada hari tertentu, yang bisa berupa 0 (sering), 1, 2, dan seterusnya.
Simulasi Monte Carlo
Discrete Distribution juga dapat dilihat pada simulasi Monte Carlo. Simulasi Monte Carlo adalah teknik pemodelan yang mengidentifikasi kemungkinan hasil yang berbeda melalui teknologi terprogram. Hal ini terutama digunakan untuk membantu memperkirakan skenario dan mengidentifikasi risiko.
Perhitungan Discrete Probability Distribution
Cara Anda menghitung Discrete Probability Distribution bergantung pada pengujian Anda, apa yang ingin Anda ukur, dan cara Anda mengukurnya. Misalnya, jika Anda melempar koin dua kali, kemungkinan kombinasinya adalah:
- Tails/tails (TT)
- Heads/tails (HT)
- Tails/heads (TH)
- Heads/heads (HH)
Karena Anda melempar koin dua kali dan ada dua kemungkinan hasil, maka ada empat kemungkinan. Masing-masing hasil mewakili seperempat kemungkinan. Kombinasi HT dan TH masing-masing berukuran seperempat (dan pada dasarnya sama), mewakili setengah hasil. Oleh karena itu, kemungkinannya adalah seperempat dari waktu tersebut, Anda akan mendapatkan TT atau HH, dan setengah dari waktu tersebut, Anda akan mendapatkan HT atau TH.
Cara kerjanya serupa untuk melempar dua dadu karena hasil pelemparan dadu bersifat diskrit. Terdapat 36 kemungkinan karena setiap dadu mempunyai enam sisi, namun tidak boleh ada hasil yang memiliki satu karena angka terendah pada setiap dadu adalah satu. Jadi hasil terendah yang bisa Anda peroleh adalah dua, dan tertinggi adalah 12. Banyak kombinasi yang akan berulang, seperti pada contoh koin—jadi semakin banyak kemungkinan yang berulang, semakin banyak pula kejadian yang akan digambarkan.
Seperti yang terlihat pada tabel di bawah, jika Anda menjumlahkan angka hasil pelemparan dadu, Anda akan mendapatkan satu contoh di mana hasilnya adalah dua dan satu adalah 12—menciptakan peluang satu banding 36 untuk angka dua dan 12.
Hasil Pelemparan Pasangan Dadu
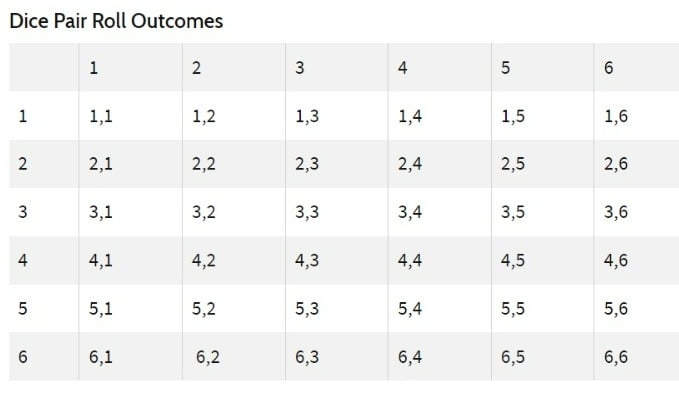
Peluang (P) bahwa X (hasilnya) akan sama dengan x (angka yang dipilih) adalah:
- P(X=2) = 1/36
- P(X=3) = 2/36
- P(X=4) = 3/36
- P(X=5) = 4/36
- P(X=6) = 5/36
- P(X=7) = 6/36
- P(X=8) = 5/36
- P(X=9) = 4/36
- P(X=10) = 3/36
- P(X=11) = 2/36
- P(X=12) = 1/36
Peluang munculnya lemparan sama dengan dua adalah satu berbanding 36; probabilitasnya sama dengan tiga adalah dua dalam 36, dan seterusnya.
Contoh Investasi
Dalam model pohon binomial di bawah ini, analis telah memilih interval tiga bulan dengan harga awal $10. Mereka telah menggunakan data masa lalu dari investasi untuk menghitung kemungkinan bahwa harga akan naik atau turun dengan cara yang sama seperti perhitungan pelemparan dadu.
Dalam gambar ini, analis menghitung bahwa probabilitas harga naik ke $12 adalah 1,03. Peluang harga akan turun menjadi $8 adalah 3,43. Dari setiap kenaikan atau penurunan harga, Anda dapat melihat para analis telah menghitung probabilitas tersendiri selama sembilan bulan. Pada akhir sembilan bulan, Anda melihat bahwa probabilitas harga saham naik menjadi $17,28 adalah nol, sedangkan probabilitas harga saham turun menjadi $7,68 adalah 4,32; kemungkinannya mencapai $5,12 adalah 6,98. Jadi, kemungkinan besar harga saham akan turun dalam sembilan bulan ke depan dibandingkan kenaikannya.

Discrete Distribution vs. Continous Distribution /Distribusi Kontinyu
Jika Discrete Distribution adalah distribusi yang menggambarkan variabel-variabel diskrit, maka distribusi kontinu adalah distribusi yang menggambarkan variabel-variabel kontinu. Perbedaannya dapat dilihat pada grafik, dimana Discrete Probability Distribution umumnya diwakili oleh batang karena datanya diskrit. Distribusi probabilitas kontinu umumnya tampak sebagai kurva atau garis pada grafik karena data di bawah garis tersebut kontinu dan tidak berhingga.
Kesimpulan
Discrete Probability Distribution adalah grafik hasil pengujian yang berhingga, seperti nilai 1, 2, 3, benar, salah, berhasil, atau gagal. Investor menggunakan distribusi probabilitas tersendiri untuk memperkirakan peluang terjadinya hasil investasi tertentu. Berbekal informasi tersebut, mereka dapat memilih strategi lindung nilai yang sesuai dengan probabilitas yang ditemukan dalam analisis mereka.
