Bell Curve adalah jenis distribusi yang umum untuk sebuah variabel, yang juga dikenal sebagai distribusi normal. Istilah “Bell Curve” berasal dari fakta bahwa grafik yang digunakan untuk menggambarkan distribusi normal terdiri dari kurva berbentuk lonceng yang simetris. Titik tertinggi pada kurva, atau bagian atas lonceng, mewakili kejadian yang paling mungkin terjadi dalam serangkaian data (rata-rata, modus, dan median dalam kasus ini), sementara semua kejadian lain yang mungkin terjadi terdistribusi secara simetris di sekitar rata-rata, menciptakan kurva yang miring ke bawah di setiap sisi puncak. Lebar Bell Curve dijelaskan oleh deviasi standarnya.
Memahami Bell Curve
Istilah “Bell Curve” digunakan untuk menggambarkan penggambaran grafis dari distribusi probabilitas normal, yang deviasi standar yang mendasari dari rata-rata menciptakan bentuk lonceng melengkung. Standar deviasi adalah pengukuran yang digunakan untuk mengukur variabilitas dispersi data, dalam satu set nilai tertentu di sekitar mean. Rata-rata, pada gilirannya, mengacu pada rata-rata semua titik data dalam kumpulan atau urutan data dan akan ditemukan pada titik tertinggi pada Bell Curve. Analis keuangan dan investor sering menggunakan distribusi probabilitas normal saat menganalisis pengembalian sekuritas atau sensitivitas pasar secara keseluruhan. Di bidang keuangan, deviasi standar yang menggambarkan imbal hasil sekuritas dikenal sebagai volatilitas. Contohnya, saham yang menunjukkan Bell Curve biasanya adalah saham blue-chip dan saham yang memiliki volatilitas lebih rendah serta pola perilaku yang lebih mudah diprediksi. Investor menggunakan distribusi probabilitas normal dari imbal hasil saham di masa lalu untuk membuat asumsi mengenai imbal hasil yang diharapkan di masa depan. Selain para guru yang menggunakan Bell Curve saat membandingkan nilai ujian, Bell Curve juga sering digunakan dalam dunia statistik yang dapat diterapkan secara luas. Bell Curve juga terkadang digunakan dalam manajemen kinerja, dengan menempatkan karyawan yang melakukan pekerjaan mereka secara rata-rata dalam distribusi normal grafik. Karyawan yang berkinerja tinggi dan karyawan yang berkinerja rendah diwakili di kedua sisi dengan kemiringan yang menurun. Hal ini dapat berguna bagi perusahaan besar ketika melakukan tinjauan kinerja atau ketika membuat keputusan manajerial.
Contoh Bell Curve
Lebar Bell Curve ditentukan oleh deviasi standar, yang dihitung sebagai tingkat variasi data dalam sampel di sekitar rata-rata. Dengan menggunakan aturan empiris, misalnya, jika 100 nilai ujian dikumpulkan dan digunakan dalam distribusi probabilitas normal, 68% dari nilai ujian tersebut harus berada dalam satu standar deviasi di atas atau di bawah rata-rata. Memindahkan dua standar deviasi dari rata-rata harus mencakup 95% dari 100 nilai tes yang dikumpulkan. Memindahkan tiga standar deviasi dari rata-rata harus mewakili 99,7% dari nilai (lihat gambar di atas).
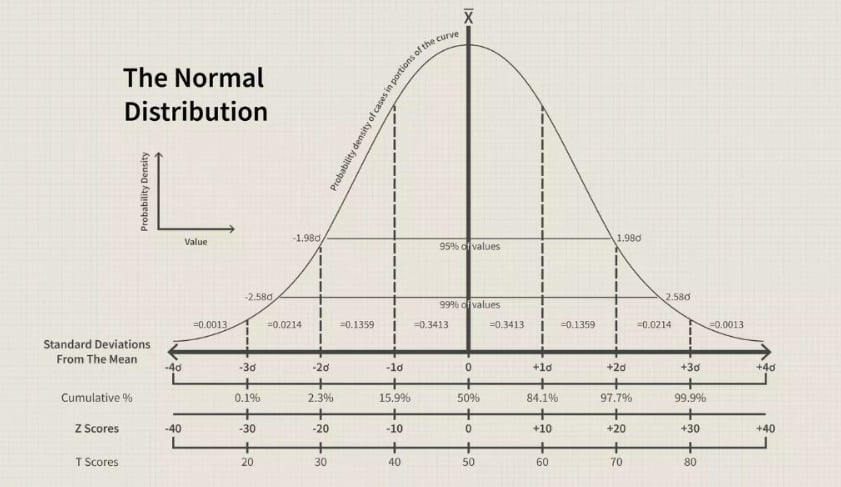
Nilai tes yang merupakan pencilan ekstrim, seperti nilai 100 atau 0, akan dianggap sebagai titik data ekor panjang yang akibatnya berada tepat di luar rentang tiga standar deviasi.
Bell Curve vs Distribusi Non-Normal
Asumsi distribusi probabilitas normal tidak selalu berlaku di dunia keuangan. Saham dan sekuritas lainnya terkadang menampilkan distribusi non-normal yang tidak menyerupai Bell Curve. Distribusi non-normal memiliki ekor yang lebih gemuk daripada distribusi Bell Curve (probabilitas normal). Ekor yang lebih gemuk memberikan sinyal negatif kepada investor bahwa ada kemungkinan lebih besar untuk mendapatkan hasil negatif.
Keterbatasan Bell Curve
Penilaian atau penilaian kinerja menggunakan Bell Curve memaksa kelompok orang untuk dikategorikan sebagai buruk, rata-rata, atau baik. Untuk kelompok yang lebih kecil, harus mengkategorikan sejumlah individu dalam setiap kategori agar sesuai dengan Bell Curve akan merugikan individu tersebut. Karena terkadang, mereka semua mungkin hanya pekerja atau siswa yang rata-rata atau bahkan baik, tetapi karena kebutuhan untuk menyesuaikan peringkat atau nilai mereka dengan Bell Curve, beberapa individu dipaksa untuk masuk ke dalam kelompok yang buruk. Pada kenyataannya, data tidak sepenuhnya normal. Terkadang ada kemiringan, atau kurangnya simetri, antara nilai yang berada di atas dan di bawah rata-rata. Di lain waktu, terdapat ekor yang gemuk (kurtosis berlebih), sehingga kejadian ekor lebih mungkin terjadi daripada yang diprediksi oleh distribusi normal.
