Binomial Option Pricing Model adalah metode penilaian opsi yang dikembangkan pada tahun 1979. Binomial Option Pricing Model menggunakan prosedur berulang, yang memungkinkan spesifikasi node, atau titik waktu, selama rentang waktu antara tanggal penilaian dan tanggal kedaluwarsa opsi. Model ini mengurangi kemungkinan perubahan harga dan menghilangkan kemungkinan arbitrase. Contoh pohon binomial yang disederhanakan mungkin terlihat seperti ini:

Dasar-dasar Binomial Option Pricing Model
Pada model harga opsi binomial, asumsinya adalah bahwa ada dua hasil yang mungkin terjadi – oleh karena itu, bagian binomial dari model tersebut. Dengan model penetapan harga, dua hasil tersebut adalah naik atau turun. Keuntungan utama dari Binomial Option Pricing Model adalah model ini sederhana secara matematis. Namun model ini dapat menjadi kompleks dalam model multi periode. Berbeda dengan model Black-Scholes, yang memberikan hasil numerik berdasarkan input, model binomial memungkinkan perhitungan aset dan opsi untuk beberapa periode bersama dengan kisaran hasil yang mungkin untuk setiap periode (lihat di bawah). Keuntungan dari tampilan multi periode ini adalah pengguna dapat memvisualisasikan perubahan harga aset dari periode ke periode dan mengevaluasi opsi berdasarkan keputusan yang dibuat pada titik waktu yang berbeda. Untuk opsi yang berbasis di Amerika Serikat, yang dapat dieksekusi kapan saja sebelum tanggal kadaluarsa, model binomial dapat memberikan informasi mengenai kapan sebaiknya opsi tersebut dieksekusi dan kapan sebaiknya opsi tersebut disimpan untuk jangka waktu yang lebih lama. Dengan melihat pohon nilai binomial, seorang pedagang dapat menentukan terlebih dahulu kapan keputusan untuk melaksanakan opsi dapat dilakukan. Jika opsi memiliki nilai positif, maka ada kemungkinan untuk di-exercise, sedangkan jika opsi memiliki nilai kurang dari nol, maka opsi tersebut harus ditahan untuk jangka waktu yang lebih lama.
Menghitung Harga dengan Model Binomial
Metode dasar untuk menghitung model opsi binomial adalah dengan menggunakan probabilitas yang sama setiap periode untuk keberhasilan dan kegagalan hingga opsi berakhir. Namun, seorang trader dapat memasukkan probabilitas yang berbeda untuk setiap periode berdasarkan informasi baru yang diperoleh seiring berjalannya waktu. Pohon binomial adalah alat yang berguna ketika menentukan harga opsi Amerika dan opsi tertanam. Kesederhanaannya merupakan kelebihan dan kekurangannya pada saat yang bersamaan. Pohon ini mudah dibuat modelnya secara mekanis, tetapi masalahnya terletak pada nilai yang mungkin diambil oleh aset acuan dalam satu periode waktu. Dalam model pohon binomial, aset yang mendasari hanya dapat bernilai tepat satu dari dua nilai yang mungkin, yang tidak realistis, karena aset dapat bernilai berapa pun dalam rentang tertentu. Contohnya, mungkin ada peluang 50/50 bahwa harga aset acuan dapat naik atau turun 30 persen dalam satu periode. Namun, untuk periode kedua, probabilitas bahwa harga aset acuan akan meningkat dapat meningkat menjadi 70/30. Contohnya, jika seorang investor mengevaluasi sebuah sumur minyak, investor tersebut tidak yakin berapa nilai sumur minyak tersebut, tetapi ada peluang 50/50 bahwa harganya akan naik. Jika harga minyak naik pada Periode 1 membuat sumur minyak lebih berharga dan fundamental pasar sekarang menunjukkan kenaikan harga minyak yang berkelanjutan, probabilitas apresiasi harga lebih lanjut mungkin sekarang menjadi 70 persen. Model binomial memungkinkan fleksibilitas ini; model Black-Scholes tidak.
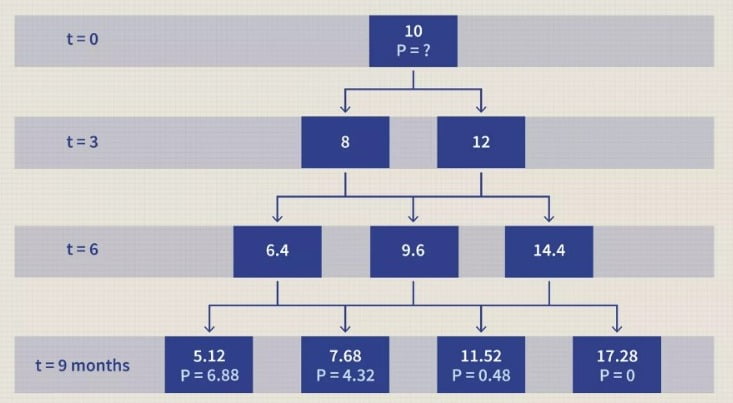
Contoh Dunia Nyata dari Binomial Option Pricing Model
Contoh pohon binomial yang disederhanakan hanya memiliki satu langkah. Asumsikan ada sebuah saham yang dihargai $100 per saham. Dalam satu bulan, harga saham ini akan naik sebesar $10 atau turun sebesar $10, sehingga menciptakan situasi berikut:
- Harga saham = $100
- Harga saham dalam satu bulan (keadaan naik) = $110
- Harga saham dalam satu bulan (keadaan turun) = $90
Selanjutnya, asumsikan ada sebuah opsi beli yang tersedia untuk saham ini yang akan berakhir dalam satu bulan dan memiliki harga kesepakatan $100. Pada kondisi naik, opsi ini bernilai $10, dan pada kondisi turun bernilai $0. Model binomial dapat menghitung berapa harga opsi call hari ini.
Untuk tujuan penyederhanaan, asumsikan bahwa seorang investor membeli satu setengah bagian saham dan menulis atau menjual satu call option. Total investasi hari ini adalah harga setengah saham dikurangi harga opsi, dan kemungkinan hasil yang akan diperoleh pada akhir bulan adalah:
- Biaya hari ini = $50 – harga opsi
- Nilai portofolio (kondisi naik) = $55 – maksimal ($110 – $100, 0) = $45
- Nilai portofolio (keadaan turun) = $45 – maksimal ($90 – $100, 0) = $45
Hasil portofolio tetap sama, tidak peduli bagaimana harga saham bergerak. Dengan hasil ini, dengan asumsi tidak ada peluang arbitrase, investor harus mendapatkan tingkat bebas risiko selama sebulan. Biaya hari ini harus sama dengan hasil yang didiskontokan pada tingkat bebas risiko selama satu bulan. Persamaan yang harus diselesaikan adalah sebagai berikut:
- Harga opsi = $50 – $45 x e ^ (-tingkat bebas risiko x T), di mana e adalah konstanta matematika 2,7183.
Dengan mengasumsikan tingkat suku bunga bebas risiko sebesar 3% per tahun, dan T sama dengan 0,0833 (satu dibagi 12), maka harga opsi beli hari ini adalah $5,11.
Binomial Option Pricing Model memberikan dua keuntungan bagi penjual opsi dibandingkan model Black-Scholes. Yang pertama adalah kesederhanaannya, yang memungkinkan lebih sedikit kesalahan dalam aplikasi komersial. Yang kedua adalah operasi berulangnya, yang menyesuaikan harga secara tepat waktu sehingga mengurangi kesempatan bagi pembeli untuk menjalankan strategi arbitrase.
Sebagai contoh, karena ia menyediakan aliran penilaian untuk turunan untuk setiap simpul dalam rentang waktu tertentu, ia berguna untuk menilai turunan seperti opsi Amerika – yang dapat dieksekusi kapan saja antara tanggal pembelian dan tanggal kedaluwarsa. Model ini juga jauh lebih sederhana dibandingkan model penetapan harga lainnya seperti model Black-Scholes.


