Duration/ Durasi dapat mengukur berapa lama waktu yang dibutuhkan, dalam beberapa tahun, bagi investor untuk mendapatkan pembayaran kembali harga obligasi berdasarkan total arus kas obligasi. Duration juga dapat mengukur sensitivitas harga obligasi atau portofolio pendapatan tetap terhadap perubahan suku bunga. Duration suatu obligasi mudah tertukar dengan jangka waktu atau waktu jatuh temponya karena jenis pengukuran Duration tertentu juga dihitung dalam satuan tahun. Namun, jangka waktu obligasi adalah ukuran linier dari tahun-tahun sampai jatuh tempo pembayaran pokok; itu tidak berubah seiring dengan lingkungan suku bunga. Sebaliknya, Durationnya bersifat nonlinier dan semakin cepat seiring dengan semakin berkurangnya waktu menuju kedewasaan.
Tujuan Duration
Duration adalah ukuran sensitivitas harga suatu obligasi atau instrumen utang lainnya terhadap perubahan suku bunga. Secara umum, semakin tinggi Durationnya, harga obligasi akan semakin turun seiring kenaikan suku bunga (dan semakin besar risiko suku bunga). Misalnya, jika suku bunga naik 1%, obligasi atau dana obligasi dengan jangka waktu rata-rata lima tahun kemungkinan akan kehilangan sekitar 5% nilainya.
Faktor-faktor tertentu dapat mempengaruhi Duration obligasi, termasuk:
- Waktu jatuh tempo: Semakin lama jatuh tempo, semakin tinggi Durationnya, dan semakin besar risiko suku bunga. Pertimbangkan dua obligasi yang masing-masing menghasilkan 5% dan berharga $1.000, namun memiliki jatuh tempo berbeda. Obligasi yang jatuh temponya lebih cepat—katakanlah, dalam satu tahun—akan melunasi biaya sebenarnya lebih cepat dibandingkan obligasi yang jatuh tempo dalam 10 tahun. Akibatnya, obligasi yang jatuh temponya lebih pendek akan memiliki Duration yang lebih rendah dan risiko yang lebih kecil.
- Tingkat kupon: Tingkat kupon obligasi merupakan faktor kunci dalam Duration perhitungan. Jika kita memiliki dua obligasi yang identik kecuali tingkat kuponnya, obligasi dengan tingkat kupon yang lebih tinggi akan membayar kembali biaya aslinya lebih cepat dibandingkan obligasi dengan imbal hasil yang lebih rendah. Semakin tinggi tingkat kupon, semakin rendah Durationnya, dan semakin rendah risiko suku bunga.
Apa Jenis Duration yang Berbeda?
Duration suatu ikatan dalam praktiknya dapat merujuk pada dua hal yang berbeda. Duration Macaulay adalah waktu rata-rata tertimbang hingga seluruh arus kas obligasi dilunasi. Dengan memperhitungkan nilai sekarang dari pembayaran obligasi di masa depan, Duration Macaulay membantu investor mengevaluasi dan membandingkan obligasi terlepas dari jangka waktu atau waktu jatuh temponya.
Jenis Duration kedua disebut Duration yang dimodifikasi. Berbeda dengan Duration Macaulay, Duration yang dimodifikasi tidak diukur dalam tahun. Duration yang dimodifikasi mengukur perkiraan perubahan harga obligasi terhadap perubahan suku bunga sebesar 1%.
Untuk memahami Duration yang dimodifikasi, perlu diingat bahwa harga obligasi dikatakan memiliki hubungan terbalik dengan suku bunga. Oleh karena itu, kenaikan suku bunga menunjukkan bahwa harga obligasi kemungkinan besar akan turun, sedangkan penurunan suku bunga menunjukkan bahwa harga obligasi kemungkinan besar akan naik.
Duration Macaulay
Duration Macaulay menemukan nilai sekarang dari pembayaran kupon obligasi di masa depan dan nilai jatuh tempo. Untungnya bagi investor, ukuran ini merupakan titik data standar di sebagian besar perangkat lunak pencarian dan analisis obligasi. Karena Duration Macaulay merupakan fungsi parsial dari waktu jatuh tempo, semakin besar Durationnya, semakin besar pula risiko suku bunga atau imbalan terhadap harga obligasi.
Duration Macaulay dapat dihitung secara manual sebagai berikut:

Di mana:
f = nomor arus kas
CF = jumlah arus kas
y = hasil hingga jatuh tempo
k = periode gabungan per tahun
Tf = waktu dalam tahun sampai arus kas diterima
PV = nilai sekarang dari seluruh arus kas
Rumus sebelumnya dibagi menjadi dua bagian. Bagian pertama digunakan untuk mencari nilai sekarang dari seluruh arus kas obligasi masa depan. Bagian kedua menemukan waktu rata-rata tertimbang hingga arus kas tersebut dibayarkan. Ketika bagian-bagian ini digabungkan, mereka memberi tahu investor jumlah rata-rata tertimbang waktu untuk menerima arus kas obligasi.
Contoh Perhitungan Duration Macaulay
Bayangkan obligasi tiga tahun dengan nilai nominal $100 yang membayar kupon 10% setiap semester ($5 setiap enam bulan) dan memiliki imbal hasil hingga jatuh tempo (YTM) sebesar 6%. Untuk mencari Duration Macaulay, langkah pertama adalah menggunakan informasi ini untuk mencari nilai sekarang dari seluruh arus kas masa depan seperti yang ditunjukkan pada tabel berikut:
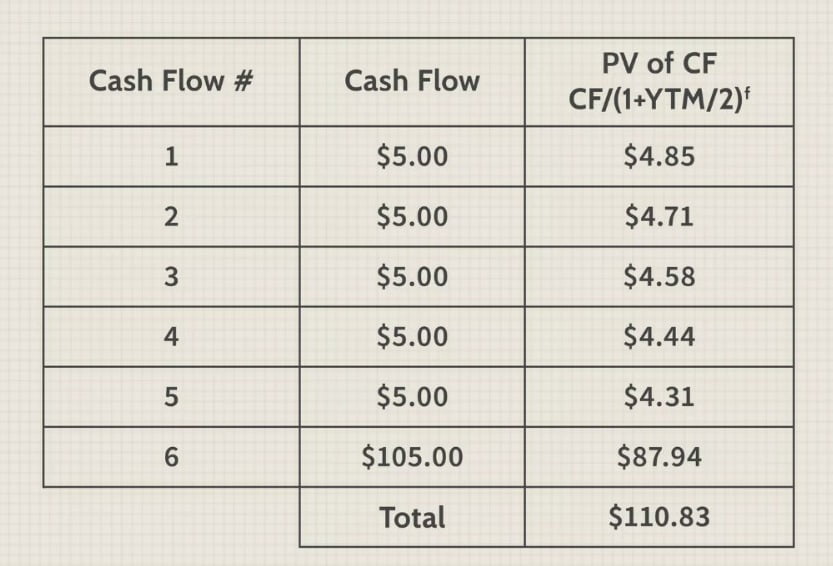
Bagian perhitungan ini penting untuk dipahami. Namun, hal tersebut tidak perlu dilakukan jika Anda sudah mengetahui YTM obligasi tersebut dan harganya saat ini. Hal ini benar karena, menurut definisi, harga obligasi saat ini adalah nilai sekarang dari seluruh arus kasnya. Untuk menyelesaikan perhitungannya, investor perlu mengambil nilai sekarang dari setiap arus kas, membaginya dengan total nilai sekarang dari seluruh arus kas obligasi dan kemudian mengalikan hasilnya dengan waktu jatuh tempo dalam beberapa tahun. Perhitungan ini lebih mudah dipahami pada tabel berikut.

Baris “Total” pada tabel memberi tahu investor bahwa obligasi tiga tahun ini memiliki Duration Macaulay selama 2,684 tahun. Pedagang mengetahui bahwa semakin lama jangka waktunya, semakin sensitif obligasi tersebut terhadap perubahan suku bunga. Jika YTM naik maka nilai obligasi yang jatuh temponya 20 tahun akan turun lebih jauh dibandingkan nilai obligasi yang jatuh temponya lima tahun. Seberapa besar perubahan harga obligasi untuk setiap 1% kenaikan atau penurunan YTM disebut Duration yang dimodifikasi.
Duration yang Dimodifikasi
Duration obligasi yang dimodifikasi membantu investor memahami seberapa besar harga obligasi akan naik atau turun jika YTM naik atau turun sebesar 1%. Ini merupakan angka penting jika investor khawatir akan perubahan suku bunga dalam jangka pendek. Modifikasi Duration obligasi dengan pembayaran kupon setengah tahunan dapat diketahui dengan rumus berikut:
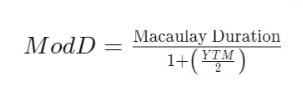
Dengan menggunakan angka-angka dari contoh sebelumnya, Anda dapat menggunakan rumus Duration yang dimodifikasi untuk mengetahui seberapa besar perubahan nilai obligasi jika terjadi perubahan suku bunga sebesar 1%, seperti yang ditunjukkan di bawah ini:
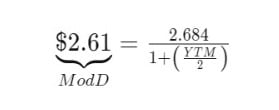
Dalam kasus ini, jika YTM meningkat dari 6% menjadi 7% karena kenaikan suku bunga, nilai obligasi akan turun sebesar $2,61. Demikian pula, harga obligasi akan naik sebesar $2,61 jika YTM turun dari 6% menjadi 5%. Sayangnya, seiring dengan perubahan YTM, laju perubahan harga juga akan meningkat atau menurun. Percepatan perubahan harga obligasi seiring naik dan turunnya suku bunga disebut konveksitas.
